文章详情

今天看到一道面试题，优化一个函数。

function fei($n) {
    if ($n == 1 || $n == 2) {
        return 1;
    }
    return fei($n - 1) + fei($n - 2);
}

起初不知道这个函数的作用，后面查了一下才知道。这个函数可以求大名鼎鼎的“斐波拉契数列”。

返回到正题上，先说说什么是递归。

递归是指函数/过程/子程序在运行过程序中直接或间接调用自身而产生的重入现象。即递归是一个过程：函数不断引用自身，直到引用的对象已知。

递归有四大原则。

1. 基准情形： 必须有某些基准情形，它无需递归即可解出。

2. 不断推进： 对于需要递归求解的情形，每次递归调用都必须使得求解状况朝着基准情形推进。

3. 设计法则： 假设所有的递归调用都能运行。

4. 合成效益法则：在求解一个问题的同一实例时，切勿在不同的递归调用中做重复性工作。 

其中第四点在递归的效率中至为关键。这是为什么用递归实现斐波那契数列的常规方法时效率很低的原因，而在二叉树中表现相当优良的原因！

什么是斐波那契数列。

斐波那契数列 又称为“兔子数列”，指的是这样一个数列：1、1、2、3、5、8、13、21、34、……在数学上，斐波纳契数列以如下被以递归的方法定义：F(0)=0，F(1)=1, F(n)=F(n-1)+F(n-2)，即从第三项开始每一项都等于前面两项的和。

global $n1;
function fei($n){
    $GLOBALS['n1']++;
    if($n==1 || $n==2){//基准情形，法则1
        return 1;
    }
    return fei($n-1) + fei($n-2); //通过调用自身，不断推进直到达到基准情形，法则2,3
}

通过观察上面的代码，我们发现一个问题，当给定一个数N时，需要先计算N-1 和N-2的情况，但是在计算N-1时同样要用计算N-2的情况，每个递归调用都触发另外两个递归调用，而这两个调用的任何一个又将调用另外连个递归调用，这样冗余计算的增量是非常快的，例如图：

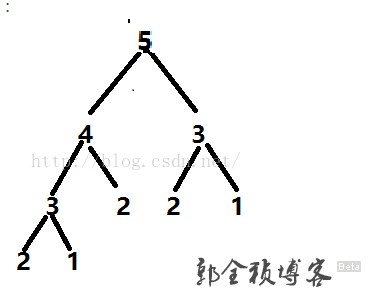
再计算 fib(5)时，需要先求fib(4)和fib(3)，

而求fib(4)时又要求fib(3)和fib(2)以此类推这样就做了大量重复计算造成了不必要的浪费，如果我们能把fib(3),fib(2),fib(1)计算好的数据先存起来，下次需要计算时直接调用就可以省去大量的重复计算，因而有了下面的优化方式：

global $n2;
function fei2($a,$b,$n){
    $GLOBALS['n2']++;
    if($n>2){
        return fei2(intval($a+$b),$a,$n-1);  //将本次计算的结果和上次计算的结果作为参数传入下一次计算中，以减少重复计算。第四法则  
    }
    return $a;
}

代码执行效果：

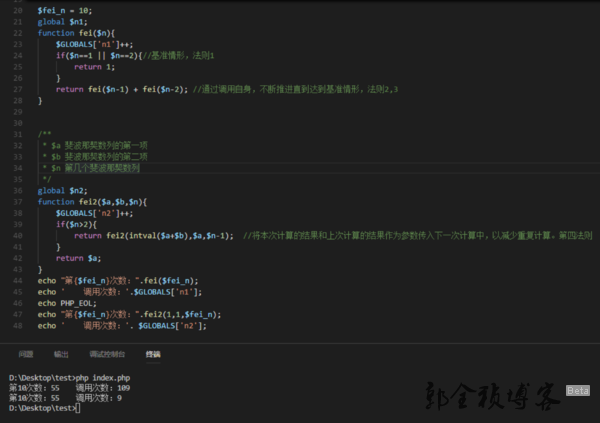
同时求第十位数值，未优化的递归函数执行了109次，而优化后的仅仅执行了9次，大大的减少了重复的计算，符合了递归调用的第四法则。

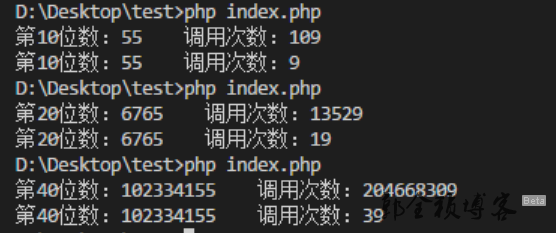
并且随着所求位数的增大执行数的差别会成几何倍的速度增加。